Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

преобразования логических выражений

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных. В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

1. Закон двойного отрицания:

А = 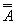. Двойное отрицание исключает отрицание.

2. Переместительный (коммутативный) закон:

— для логического сложения: А к B = B к A ;

— для логического умножения: A & B = B & A .

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

В обычной алгебре a + b = b + a, a Д b = b Д a.

3. Сочетательный (ассоциативный) закон:

— для логического сложения: ( A к B ) к C = A к ( B к C );

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

В обычной алгебре: (a + b) + c = a + (b + c) = a + b + c,

а Д ( b Д c ) = a Д ( b Д c ) = a Д b Д c .

4. Распределительный (дистрибутивный) закон:

— для логического сложения: ( A к B )& C = ( A & C ) к ( B & C );

— для логического умножения: ( A & B ) к C = ( A к C )&( B к C ).

Определяет правило выноса общего высказывания за скобку.

В обычной алгебре: (a + b) Д c = a Д c + b Д c.

5. Закон общей инверсии (законы де Моргана):

— для логического сложения = & ;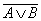

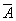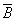— для логического умножения: 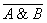= 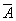к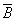

6. Закон идемпотентности ( от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):

— для логического сложения: A к A = A ;

— для логического умножения: A & A = A .

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

— для логического сложения: A к 1 = 1, A к 0 = A ;

— для логического умножения: A &1 = A , A &0 = 0.

8. Закон противоречия: A& 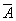= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего: A к 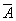= 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

— для логического умножения: A &( A к B ) = A .

11. Закон исключения (склеивания):

— для логического сложения: ( A & B ) к ( 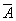& B ) = B ;

— для логического умножения: ( A к B )&( 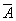к B ) = B .

12. Закон контрапозиции (правило перевертывания): ( A л B ) = ( B л A ).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

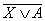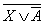Пример. Найдите X, если к = В.

Для преобразования левой части равенства последовательно воспользуемся законом де Моргана для логического сложения и законом двойного отрицания:

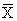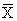( & ) к ( & A )

Согласно распределительному закону для логического сложения:

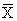&( к A )

Согласно закону исключения третьего и закона исключения констант:

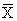&1 =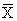

Полученную левую часть приравняем правой:

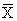= В

Окончательно получим, что X = .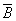

Пример 2. Упростите логическое выражение ( A к B к C )&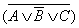

Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения.

Согласно закону общей инверсии для логического сложения (первому закону Моргана) и закону двойного отрицания:

( A к B к C )& 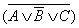= ( A к B к C )&( & B & )

Согласно распределительному (дистрибутивному) закону для логического сложения:

(A к B к C )&( &B& ) = (A& ) к (B& ) к (C& ) к (A&B) к (B&B) к (C&B) к (A& ) к (B& ) к (C& )

Согласно закона противоречия: ( A & ) = 0; ( C & ) = 0

Согласно закона идемпотентности ( B & B ) = B

Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем:

0 к ( A & B ) к ( & B ) к B к ( C & B ) к ( & B ) к ( C & ) к ( A & ) к 0

Согласно закона исключения (склеивания)

( A & B ) к ( & B ) = B

( C & B ) к ( & B ) = B

Подставляем значения и получаем:

0 к B к B к B к ( C & ) к ( A & ) к 0

Согласно закона исключения констант для логического сложения и закона идемпотентности:

Подставляем значения и получаем:

B к ( C & ) к ( A & )

Согласно распределительному (дистрибутивному) закону для логического умножения:

( C & ) к ( A & ) = ( C к A )&( C к )&( к A )&( к )

Согласно закона исключения третьего: ( C к ) = 1 ( к A ) = 1

Подставляем значения и окончательно получаем: B & & .

Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г.

Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ и задаётся следующей таблицей истинности:

Таким образом, высказывание «X ↓ Y» означает «ни X, ни Y». От перемены мест операндов результат операции не изменяется.

11. Штрих Ше́ффера — бинарнаялогическая операция,булева функциянад двумя переменными. Введена в рассмотрениеГенри Шефферомв 1913 г. (вотдельных источниках именуется как Пунктир Чулкова) Штрих Шеффера, обычно обозначаемый |, эквивалентен операции И-НЕ и задаётся следующей таблицей истинности:

Таким образом, высказывание X | Y означает, что X и Y несовместны, т.е. не являются истинными одновременно. От перемены мест операндов результат операции не изменяется. Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть используя только штрих Шеффера можно построить остальные операции. Например,

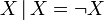—отрицание

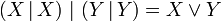— дизъюнкция

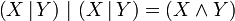— конъюнкция

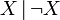— константа 1

В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.

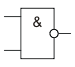
Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера обозначается следующим образом (по стандартам ANSI):

В европейских стандартах принято другое обозначение:

12. Диодные ключи. Общие сведения. Электронный ключ — это устройство, которое может находиться в одном из двух устойчивых состояний: замкнутом или разомкнутом. Основу электронного ключа составляет нелинейный активный элемент (полупроводниковый диод, транзистор, тиристор и др.), работающий в ключевом режиме. По типу используемого нелинейного элемента электронные ключи делятся на диодные, транзисторные, тиристорные и т. д.

Диодные ключи. Простейший тип электронных ключей – диодные ключи. В качестве активных элементов в них используются полупроводниковые или электровакуумные диоды.

При положительном входном напряжении диод открыт и ток через него

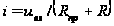, где 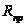– прямое сопротивление диода.

.

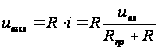Обычно 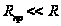, тогда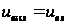. При отрицательном входном напряжении ток идет через диод

,

где – обратное сопротивление диода.

При этом выходное напряжение

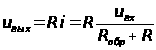. Как правило, 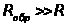и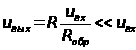. При изменении полярности включения диода график функции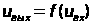повернется на угол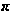вокруг начала координат.

Диодные ключи не позволяют электрически разделить управляющую и управляемые цепи, что часто требуется на практике. Для переключения (коммутации) напряжений и токов служат т.н. диодные ключи. Эти схемы позволяют при подаче определенного управляющего напряжения замыкать/размыкать электрическую цепь, по которой передается полезный сигнал (ток, напряжение). В простейших ключевых схемах в качестве управляющего может использоваться сам входной сигнал.

Говоря о диодных ключах нельзя не упомянуть особый класс полупроводниковых диодов — p-i-n-диоды. Они применяются только для коммутации ВЧ и СВЧ сигналов. Это возможно благодаря их уникальному свойству — регулируемой проводимости на частоте сигнала. Такое регулирование осуществляется обычно либо при подаче на диод внешнего постоянного напряжения смещения, либо непосредственно уровнем сигнала (для ограничительных p-i-n-диодов).

Тема 22. Законы алгебры логики в ОФПС и их следствия. Правило выполнения совместных логических действий, правило склеивания, правило поглощения, правило развертывания

В алгебре логики имеются четыре основных закона, регламентирующих порядок производства операций НЕ, И, ИЛИ в любом логическом выражении:

инверсии (правило Де Моргана).

Переместительный закон. Этот закон справедлив как для дизъюнкции, так и для конъюнкции:

Справедливость выражения (1) нетрудно доказать простой подстановкой в него различных значений x₁ и x₂. Поскольку любую перестановку большего количества слагаемых можно свести к последовательности перестановок слагаемых в отдельных парах, то переместительный закон будет справедлив при любом числе слагаемых.

Сочетательный закон. Этот закон, так же как и переместительный, является симметричным, т. е. справедливым и для дизъюнкции, и для конъюнкции:

Доказательство этого закона также не представляет никаких трудностей и может быть выполнено простой подстановкой.

Распределительный закон. В отличие от обычной алгебры алгебра логики симметрична. В ней справедливы два распределительных закона:

для логического умножения относительно логического сложения (распределительный закон 1-го рода) и для логического сложения относительно логического умножения (распределительный закон 2-го рода).

1. Распределительный закон 1-го рода записывается следующим образом:

Справедливость формулы (3), а также и ее более общего случая, когда в скобках заключена сумма любого количества слагаемых, можно доказать путем установления идентичности условий обращения в 0 или 1 ее левой и правой частей. Условием обращения в нуль левой части выражения (3) состоит в том, чтобы нулю равнялся либо один аргумент х₃, либо одновременно аргументы x₁ и x₂. Условия обращения в нуль правой части выражения (1) такие же. Следовательно, распределительный закон 1-го рода справедлив для алгебры логики.

2. Распределительный закон 2-го рода имеет вид

Справедливость формулы (4) (при любом количестве аргументов) нетрудно доказать посредством установления идентичности условий обращения обеих ее частей в единицу.

Закон инверсии (правило Де Моргана). Этот закон, так же как и все предыдущие, симметричен относительно логических сложения и умножения.

1. Отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:

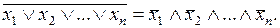(5)

Доказательство закона не представляет трудностей, поскольку условие обращения в нуль как левой, так и правой частей выражения (5) состоит в том, чтобы был истинным хотя бы один аргумент.

2. Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов:

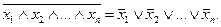(6)

Справедливость этого закона следует из того, что условие обращения в единицу обеих частей формулы (6) заключается в том, чтобы был ложным хотя бы один аргумент.

Следствия из законов алгебры логики. Из доказанных выше законов можно вывести ряд следствий, которые сформулируем в виде правил.

Правило выполнения совместных логических действий (правило старшинства логических функций). При решении логических задач приходится встречаться с выражениями, содержащими действия отрицания, конъюнкции и дизъюнкции в любом сочетании. По аналогии с арифметическими действиями будем считать отрицание логическим действием первой ступени (старшей логической операцией), конъюнкцию – действием второй ступени, а дизъюнкцию – действием третьей ступени (младшей логической операцией).

Старшинство операции инверсии вытекает из закона инверсии, в соответствии с которым логическая сумма отрицаний некоторых аргументов не равна отрицанию их суммы (это справедливо и для логического произведения). Это значит, что ни операцию дизъюнкции, ни операцию конъюнкции нельзя проводить, игнорируя знак отрицания над каким-либо из логических аргументов, т. е. операцию отрицания надо проводить в первую очередь.

Относительно операций логического сложения и умножения на основании симметричности законов алгебры логики можно сказать, что они «равноправны». Из этого следует, что можно условиться считать более старшей операцией любую из них, но, приняв какое-либо условие, надо придерживаться его все время. На практике оказалось удобнее считать более старшей операцию логического умножения, так как это соответствует правилам обычной алгебры и для нас более привычно.

На основе изложенного можно сформулировать следующее правило выполнения совместных логических действий: если в логическом выражении встречаются только действия одной и той же ступени, то их принято выполнять в том порядке, в котором они написаны; если в логическом выражении встречаются действия различных ступеней, то сначала принято выполнять действия первой ступени, затем — второй, и только после этого — третьей. Всякое отклонение от этого порядка должно быть обозначено скобками.

Правило склеивания. Если имеется некоторый конечный набор логических аргументов x₁, x₂, … x_n, то логическое произведение любого их числа называется элементарным в том случае, когда сомножителями в нем являются либо одиночные аргументы, либо отрицания одиночных аргументов. Так, например, f₁(х₁, х₂, x₃, х₄)= х₁ х₂ x₃х₄ -элементарное произведение (элементарная конъюнкция); –не является элементарным произведением.

Символ любого аргумента в элементарной конъюнкции может встречаться только один раз, поскольку произведение аргумента самого на себя равно этому же аргументу, а произведение аргумента на свое отрицание равно нулю. Количество сомножителей в элементарной конъюнкции называется ее рангом.

Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из сомножителей. Например, элементарные конъюнкции

f₁(х₁, х₂, x₃, х₄)= х₁× х₂× x₃×х₄ и f₃(х₁, х₂, x₃, х₄)=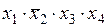

являются соседними, так как отличаются только одной инверсией в переменной x₂, а элементарные конъюнкции

f₃(х₁, х₂, x₃, х₄)= 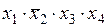и f₄(х₁, х₂, x₃, х₄)=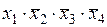

соседними не являются.

Правило склеивания для элементарных конъюнкций может быть сформулировано следующим образом: логическую сумму двух соседних произведений некоторого ранга r можно заменить одним элементарным произведением ранга r-1, являющимся общей частью исходных слагаемых.

Это правило является следствием распределительного закона 1-го рода и доказывается путем вынесения за скобку общей части слагаемых, являющихся соседними конъюнкциями. Тогда в скобках остается логическая сумма некоторого аргумента и его инверсии, равная единице, что и доказывает справедливость правила.

Поскольку алгебра логики является симметричной, то все определения, данные для конъюнкции, будут справедливы и для дизъюнкции.

Если имеется некоторый конечный набор логических аргументов, то логическая сумма (дизъюнкция), зависящая от любого их числа, называется элементарной в том случае, когда слагаемыми в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов.

Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные суммы одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из слагаемых.

Правило склеивания двух элементарных дизъюнкций формулируется так: логическое произведение двух соседних сумм некоторого ранга r можно заменить одной элементарной суммой ранга r-1, являющейся общей частью исходных сомножителей.

Это правило является следствием распределительного закона 2-го рода и применяется для упрощения логических выражений.

Например: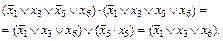

Правило поглощения. Так же как и склеивание, поглощение может быть двух видов. Правило поглощения для двух элементарных конъюнкций формулируется так: логическую сумму двух элементарных произведений разных рангов, из которых одно является собственной частью другого, можно заменить слагаемым, имеющим меньший ранг.

Это правило является следствием распределительного закона 1-го рода. Доказывается оно посредством вынесения за скобку общей части слагаемых. В скобках останется логическая сумма некоторого выражения и единицы, равная в свою очередь также единице, что и доказывает справедливость правила.

Например,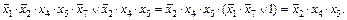

Правило поглощения для двух элементарных дизъюнкций: логическое произведение двух элементарных сумм разных рангов, из которых одна является общей частью другой, можно заменить сомножителем, имеющим меньший ранг.

Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логических функций.

Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу:

· в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п-r единиц, где п — ранг конституенты;

· каждая единица представляется в виде логической суммы некоторой, не имеющейся в исходной конъюнкции переменной и ее отрицания: ;

· производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму конституент единицы.

Пример. Развернуть элементарную конъюнкцию f(x₁,x₂,x₃,x₄) = =x₁x₃ в логическую сумму конституент единицы.

Решение. Ранг конституенты единицы для данной функции равен 4. Производим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания:

= что и требовалось получить.

Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также в три этапа по следующему правилу:

· в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей;

· каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной дизъюнкции переменной, и ее отрицания:

· получившееся выражение преобразуется на основе распределительного закона второго рода таким образом, чтобы произвести развертывание исходной элементарной дизъюнкции ранга r в логическое произведение конституент нуля.

Пример. Развернуть элементарную дизъюнкцию f(x₁,x₂,x₃,x₄)= =x₃x₄ влогическое произведение конституент нуля.

Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развертывания:

что и требовалось получить.

Проверить правильность проведенных преобразований можно при помощи правила склеивания.

109.201.143.55 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Источники:

http://lww-infproekt0405.narod.ru/Logika/Log.html
http://studfile.net/preview/3545493/page:3/
http://studopedia.ru/6_27710_tema–zakoni-algebri-logiki-v-ofps-i-ih-sledstviya-pravilo-vipolneniya-sovmestnih-logicheskih-deystviy-pravilo-skleivaniya-pravilo-pogloshcheniya-pravilo-razvertivaniya.html